The Problem: Call for Participation

New designs of smart beds are built with the ability to monitor user vitals, such as heart rate and respiration rate, and sleep characteristics, such as quality and posture. Many are familiar with how such sleep insights can be estimated from smart watches. However, smart beds are arguably a more comfortable alternative to smart watches for sleeping related insights, as they are non-contact and enable users to sleep watch-free.

One sensor that enables estimating vitals and sleep insights in beds is an accelerometer. Accelerometers are preferrable for bed-based sleep insights as they do not capture sensitive user information such as audio and video which may otherwise turn users away from wanting to use such smart beds. When subjects lay on a smart bed with an accelerometer integrated within the mattress, the expansion and contraction of their chest from breathing induces a tilt in the mattress, which is measured by the accelerometer. It has been proven that vital signs such as heart rate and respiration rate can be extracted from accelerometers attached to a subject’s chest. Expanding on this idea, we propose that such vital signs can also be estimated based on the accelerometer recordings tracking the movements of the bed.

One challenge of accelerometer-only smart beds is determining when to estimate user vitals. It is important to distinguish ambient noise arising from other vibrations of the bed from the motions arising when a user is lying on the bed. In particular, it is essential to determine if a user is lying on the bed as otherwise the inferred vitals may correspond to spurious noise signals. Additionally, the vitals produced when no one is present could cause undue concern if they are outside the normal range. Determining the presence of a person in bed is made more challenging by a variety of factors such as:

• Person-to-person variations
• Position-based variations in "in bed" signals
• Vibrations captured from external disturbances like people walking around
• Motion artifacts introduced by users adjusting their position in bed

This challenge focuses on the person detection problem. We have collected a dataset of raw accelerometer signals from an ADXL355 accelerometer, placed in between a mattress and a mattress topper. The ADXL355 is an ultra-low noise accelerometer, with a noise density of 22.5 \(\frac{\mu g}{\sqrt{Hz}}\). The dataset contains samples from a variety of users with a variety of on and off-bed disturbances. We invite participants to partake in 2 tasks:

• Task 1: Classification of pre-chunked accelerometer signals into the following categories: {"not in bed", "in bed"}
• Task 2:Streaming version of a person-detection classifier which minimizes latency and maximizes accuracy.

Intellectual property (IP) of the shared/submitted code is not transferred to the challenge organizers. Participants remain the owners of their code. If code is made publicly available by participants, an appropriate license should be added.

Dataset

The provided datasets for this challenge were collected for research purposes at the Analog Garage, an advanced research and development center within Analog Devices, as part of a research project on estimating vital signs from an accelerometer placed within a mattress. The experimental setup is shown below. An ADXL355 accelerometer is placed between a mattress and a mattress topper. An example signal generated from a subject lying still in bed is shown on the right. In this example, lower frequency data corresponding to respiration is most visible in the y-axis and higher frequency pulses associated with heart beats are most visible in the z-axis. Note however that this is only meant to be an illustrative example and is not always the case.

Our team collected timestamped acceleromter data across 42 subjects. The subjects are sometimes in bed, in varying positions, and sometimes out of bed. There are varying levels of disturbances present in the data. Each subject contributes approximately 15 minutes of data, resulting in 10.5 hours of data.

Tracks and Evaluation

Track 1: Segmented Detection

For the first challenge, we invite participants to build a person-in-bed classifier that operates on pre-chunked accelerometer samples.

Data Overview

The dataset for track 1 contains entries in the following format: $$ \begin{equation} \begin{split} \{\hspace{1 cm}&\\ \hspace{1 cm}&\texttt{`subject'} : \texttt{int}, \\ \hspace{1 cm}&\texttt{`chunk_id'} : \texttt{int}, \\ \hspace{1 cm}&\texttt{`accel'} : [[a_{0,x}, a_{0,y}, a_{0,z}], [a_{1,x}, a_{1,y}, a_{1,z}], \dots], \\ \hspace{1 cm}&\texttt{`ts'} : [t_0, t_1, \dots], \\ \hspace{1 cm}&\texttt{`label'} : \texttt{int} \\ \}\hspace{1 cm}& \end{split} \end{equation} $$ \(\texttt{subject}\) is an integer ID corresponding to the subject data was collected on. \(\texttt{chunk_id}\) is unique ID for this chunk across all chunks in the dataset. Note that there is no particular meaning to the value \(\texttt{chunk_id}\) beyond being a unique identifier (i.e. order has no meaning).

Each \(\texttt{accel}\) sample can be converted to a \( (2500,3) \) matrix, resulting from the following collection attributes:

• Sample rate 250 Hz
• Sample length 10 seconds, giving 2500 samples at the above sample rate
• Each sample is a raw 3-axis accelerometer value

We provide the timestamps associated with \(\texttt{accel}\) in the \(\texttt{ts}\) list. This is also length 2500, one timestamp per accelerometer sample. The timestamps are UTC timestamps in seconds. Finally, the attribute \(\texttt{label}\) is a single integer value, 0 for "not in bed" and 1 for "in bed".

Evaluation

The objective of this task is to maximize the balanced accuracy of the classifer. This can be computed as below: $$ Acc_{balanced} = \frac{1}{2}(TPR + TNR) $$ where \( TPR \) is the true positive rate, computed as: $$ TPR = \frac{TP}{TP + FN} $$ and \( TNR \) is the true negative rate, computed as: $$ TNR = \frac{TN}{TN + FP} $$

Track 2: Streaming Detection

In this second challenge, we invite participants to design a more practical implementation of their person-detection algorithm: a streaming-based version. The dataset for this challenge contains entire subject waveforms, approximately 15 minutes of data per subject. Participants are tasked with predicting in-bed status, causally, at each timestamp. Algorithms can make predictions utilizing windows longer than the 10 second window provided in track 1 in effort to improve accuracy, however doing so will impact latency. Shorter windows can also be considered to improve latency, however doing so may impact accuracy. Latency will be most notable when transitioning from "in bed" to "not in bed" portions and visa versa. This track is designed to evaluate the real user experience of a person detection algorithm: How accurate is the model generally? How long does the detector take to transition between class predictions when someone gets into or out of bed? Submissions should strive to maximize accuracy, while minimizing latency.

Data Overview

The dataset for track 2 contains entries in the following format: $$ \begin{equation} \begin{split} \{\hspace{1 cm}&\\ \hspace{1 cm}&\texttt{`subject'} : \texttt{int}, \\ \hspace{1 cm}&\texttt{`accel'} : [[a_{0,x}, a_{0,y}, a_{0,z}], [a_{1,x}, a_{1,y}, a_{1,z}], \dots], \\ \hspace{1 cm}&\texttt{`ts'} : [t_0, t_1, \dots], \\ \hspace{1 cm}&\texttt{`labels'} : [l_0, l_1, \dots] \\ \}\hspace{1 cm}& \end{split} \end{equation} $$ The \(\texttt{subject}\) attribute is an integer ID corresponding to the subject data was collected on (same as in track 1). The \( \texttt{accel} \) attribute contains the accelerometer samples for the entire waveform. This is generally 15 minutes of data, sometimes more or less. This can be shaped into an \( (n_{samples}, 3)\) matrix. The sample rate is the same as in track 1, 250 Hz.

\( \texttt{ts} \) and \( \texttt{labels} \) are each \( n_{samples} \) in length, containing UTC timestamps in seconds and class labels, respectively. There is now a class label at every timestamp, compared to track 1 where there was only one label for the waveform.

Rules

Participants must abide by the following rules for solutions to be considered:

1. Systems must be casual. Output at time \( t_i \) must only use samples at times \( t \leq t_i \)

Evaluation

We have come up with an evaluation metric for this track which incorporates metrics for the following objectives: minimizing latency and maximizing accuracy. Slight emphasis is placed on the former since Track 1 handles accuracy alone. A depiction of the scoring methodology is below and explained in the subsequent paragraphs.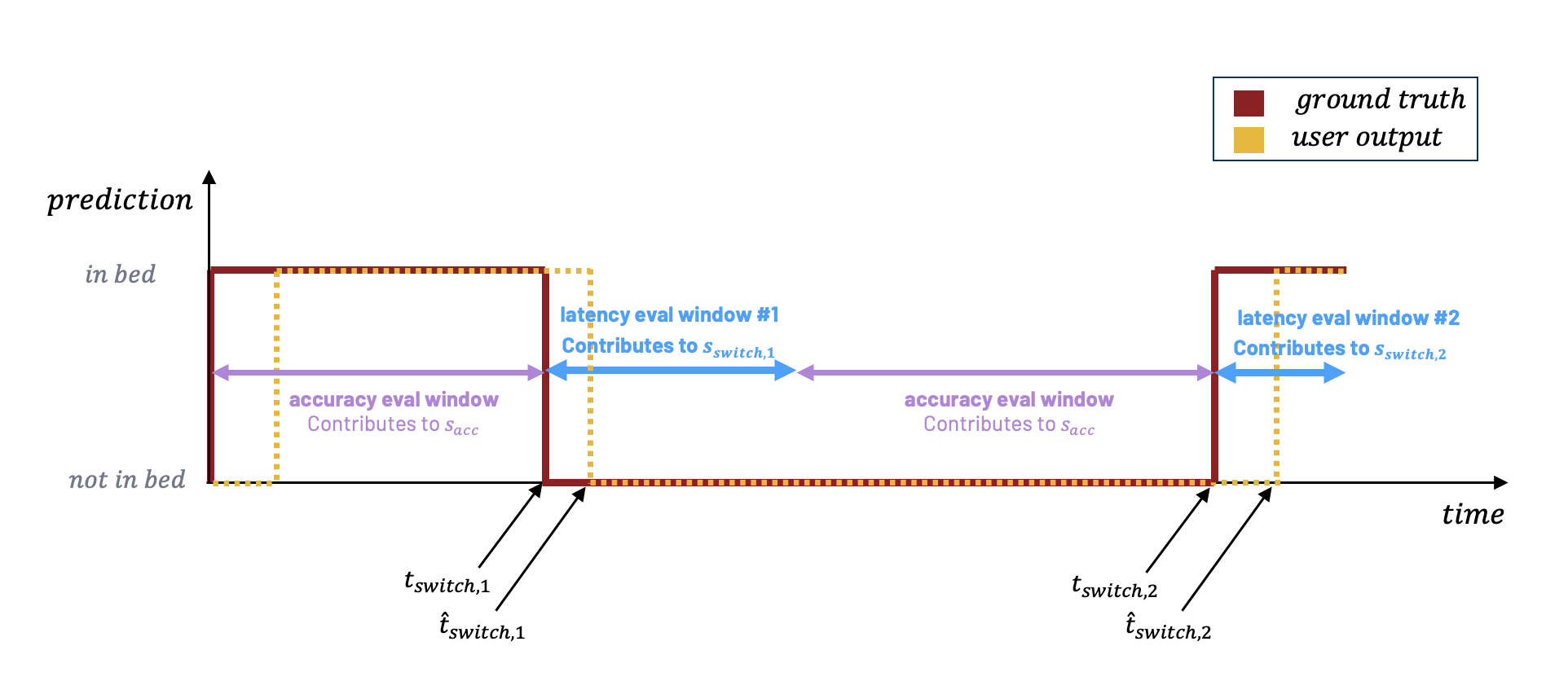 First, we will explain how we compute the score \(s_j\) for an individual subject, subject \( j\). Each waveform has a total number of transitions, denoted \( n_{switch} \), which is the number of times the subject transitions from "in bed" to "not in bed" or visa versa. For example, if a subject is in bed the entire data collection, \(n_{switch} = 0\). If the subject starts in bed, then gets out of bed and remains out of bed for the rest of the collection, \(n_{switch}=1 \). In the image above, \( n_{switch} = 2 \). The final score for a subject will be a combination of \( n_{switch} + 1 \) scores: \( s_{acc} \) which represents the accuracy score (computed outside of the latency windows only), and each \( s_{switch,i} \), which represent the score at the \(i^{th}\) transition between classes, for \(i\) in \(1, \dots, n_{switch}\): $$ s_j = \frac{s_{acc} + \sum_{i=1}^{n_{switch}}s_{switch,i}}{n_{switch}+1} $$ The accuracy \( s_{acc} \) is computed outside of the latency windows and represents general accuracy of the method. The is computed as: $$ s_{acc} = \frac{TP + TN}{TP + FP + TN + FN} $$ Each transition score \( s_{switch,i} \) is computed as a combination of the prediction latency and accuracy in the window: $$ s_{switch,i} = \frac{s_{acc,i} + s_{latency,i}}{2} $$ The latency score at transition \( i \) is evaluated as below. $$ s_{latency,i} = \exp\left(-2 \left[ ln \left(1 - \frac{(\hat{t}_{switch,i} - t_{switch,i})}{n_{win,i}}\right) \right]^2 \right) $$ In the equation above \( n_{win,i} \) is set to correspond to a 60 second window unless the number of remaining samples after \( t_{switch,i} \) is less than that.

Let us now outline the nature of \(s_{switch,i}\) as a function of the detection delay \(\Delta t_{switch, i} = (\hat{t}_{switch,i} - t_{switch,i})\). For the purpose of exposition, consider an ideal detector that switches to the correct state at \(\hat{t}_{switch,i}\) and outputs the correct state for all other samples following the transition. Then the corresponding switch score behaves as shown in following plot.

It is evident that the resultant switch score is higher for low latency detection and decreases with increasing decision delay. In particular, the switch score exceeds the accuracy score under low latency detection but is lower than that achieved by simple detection of states when the latency is higher. Thus, it is essential to ensure early detection of change points.

Determining \( \hat{t}_{switch,i} \) might be ambiguous if the submitted waveform flickers between detections during the latency window, leading to multiple position times to use. We will use the following heuristics to determine \( \hat{t}_{switch,i} \):

1. At \( \hat{t}_{switch,i} \), the predictions transition to the correct state
2. For at least 15 seconds after \( \hat{t}_{switch,i} \), the correct prediction is held
3. At least 80% of the remaining predictions in the latency window after \( \hat{t}_{switch,i} \) are estimated correctly.

We will set \( \hat{t}_{switch,i} \) to the earliest timestamp in latency window \( i \) that meets the above criteria. The reasoning for each criteria is as follows: criteria 1 ensures correct transition. Criteria 2 ensures that the transition really occured and wasn't due to a brief flicker in state. Criteria 3 ensures that the transition was meaningful/held during most of the remainder of the window. Some false positives or false negatives are allowed, but too many implies the change in state wasn't actually meanginful. If no valid \( \hat{t}_{switch,i} \) is found, then \( s_{latency,i}\) is set to 0. The parameters of 15 seconds and 80% were established based on what output would feel reasonable in a real scenario with a given person detector.

The accuracy score within the transition is computed as below for all predictions that fall in the transition window. $$ s_{acc,i} = \frac{TP + TN}{TP + FP + TN + FN} $$

The above formula is used for the predictions for each subject. It will generate a score between 0 and 1 per subject. The final score for track 2 will be the average score across all subjects: $$ s = \frac{1}{n_{subjects}}\sum_{j=1}^{n_{subjects}}s_j $$

Registration

Why we need registration: the dataset is collected with real human beings lying in the bed. We therefore need to retain ownership of the data, which means we need you to send a license before we can share the data. So we'll send you that once you register and then send you the link to the data and sample code. The dataset and submissions will be handled via Kaggle.

Please contact us to register!

Timeline

• Training dataset release: September 23, 2024
• Submission portal opens: November 18, 2024
• Submissions due: November 25, 2024
• Results announced and invitation to write a paper: December 2, 2024
• Papers due: December 9, 2024

Results